• Triangular formula expression in Pyslvs

• Source code written in Python

• Pyslvs 中的三角形表示式

• Python 版本的原始碼

Triangular formulas in Pyslvs

In order to reach the simulation of mechanism motion path, Pyslvs takes three geometric solutions to meets the joint types in PMKS.

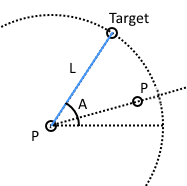
• PLA(P): Input as two (or one) known point(s), distance of reference point to the target point, and an angle value of them (or horizontal line), we can find the coordinate of target point.
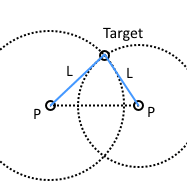
• PLLP: Input as two known points, two distances of two reference points to the target point, we can find the coordinate of target point.
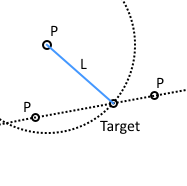
• PLPP: Input as a known point, distance of reference point to the target point, a straight line between two known points, we can find the coordinate of target point that is on the line.

為了達成機構路徑的模擬，以符合 PMKS 所能模擬的接頭種類，Pyslvs 採用三種幾何解法：

• PLA(P)：透過兩個（或一個）已知點、基準點至目標點距離，及其（與水平線）的夾角，可以求得目標點座標。
• PLLP：透過兩個已知點、兩基準點至目標點距離，可以求得目標點座標。
• PLPP：透過一個已知點、基準點至目標點距離、已知兩點連成的直線，可以求得目標點在直線上的座標。

PLAP

PLLP

PLPP

Expression

Pyslvs is using the expression to solving coordinates as below:

Pyslvs 使用函式解題的表示法如下：

Function[parameter0, parameter1, parameter2, ...](Target); ...

After determined the target point by arguments, it can be use as a parameter to calculate next formula.

For example, the coordinates of a four bar linkage mechanism can be find out with three formulas:

當透過輸入端求解之後，可以透過解出的目標點繼續求解。

例如，一個四連桿機構可以透過三個函式求解：

#Known: a0, P0, P2, L0, L1, L2, L3, L4
PLAP[P0, L0, a0](P1); PLLP[P1, L1, L2, P2](P3); PLLP[P1, L3, L4, P3](P4)

Source code

There has input and output types of Cython function, and the calculation method as Python version.

這裡提供 Cython 的輸入輸出類型與 Python 版本的運算方法。

PLAP

tuple PLAP(Coordinate A, double L0, double a0, Coordinate B=0, bool inverse=false);

def PLAP(A, L0, a0, B=None, inverse=False):
    """Point on circle by angle."""
    a1 = atan2(B.y - A.y, B.x - A.x) if B else 0
    if inverse:
        return (A.x + L0*cos(a1 - a0), A.y + L0*sin(a1 - a0))
    else:
        return (A.x + L0*cos(a1 + a0), A.y + L0*sin(a1 + a0))

PLLP

tuple PLLP(Coordinate A, double L0, double L1, Coordinate B, bool inverse=false);

def PLLP(A, L0, L1, B, inverse=False):
    """Two intersection points of two circles."""
    dx = B.x - A.x
    dy = B.y - A.y
    d = A.distance(B)

    #No solutions, the circles are separate.
    if d > L0 + L1:
        return (nan, nan)

    #No solutions because one circle is contained within the other.
    if d < abs(L0 - L1):
        return (nan, nan)

    #Circles are coincident and there are an infinite number of solutions.
    if (d == 0) and (L0 == L1):
        return (nan, nan)
    a = (L0*L0 - L1*L1 + d*d)/(2*d)
    h = sqrt(L0*L0 - a*a)
    xm = A.x + a*dx/d
    ym = A.y + a*dy/d

    if inverse:
        return (xm + h*dy/d, ym - h*dx/d)
    else:
        return (xm - h*dy/d, ym + h*dx/d)

PLPP

tuple PLPP(Coordinate A, double L0, Coordinate B, Coordinate C, bool inverse=false);

def PLAP(A, L0, B, C, inverse=False):
    """Two intersection points of a line and a circle."""
    line_mag = B.distance(C)
    dx = C.x - B.x
    dy = C.y - B.y
    u = ((A.x - B.x)*dx + (A.y - B.y)*dy) / (line_mag*line_mag)
    I = Coordinate(B.x + u*dx, B.y + u*dy)

    #Test distance between point A and intersection.
    d = A.distance(I)
    if d > L0:
        #No intersection.
        return (nan, nan)
    elif d == L0:
        #One intersection point.
        return (I.x, I.y)

    #Two intersection points.
    d = sqrt(L0*L0 - d*d) / line_mag
    dx *= d
    dy *= d
    if inverse:
        return (I.x - dx, I.y - dy)
    else:
        return (I.x + dx, I.y + dy)